预备知识

序偶： 两个元素a、b有序地放在一起，称为一个有序对或序偶，记以(a,b)。
序偶的特点： 两个有序对(a,b)和(c,d)相等当且仅当a=c，b=d
$(𝑎1,𝑎_2,⋯,𝑎𝑛)$:n元有序组
笛卡尔乘积
设A、B是两个集合，所有有序对(x,y)做成的集合(其中x$\in$A,y$\in$B)，称为A、B的笛卡儿积。
A$\times$B={(x,y)|x$\in$A且y$\in$B}
例： A={a,b,c}, B={1,2} $\rightarrow$A$\times$B=={(a,1),(a,2),(b,1),(b,2),(c,1),(c,2)}
性质
|A$\times$B|=|A|$\times$|B|；
笛卡儿积运算不满足交换律，即 A$\times$B$\not=$B$\times$A；
对任意集合A，有A$\times $\varnothing$=$\varnothing$，$\varnothing$ \times$A=$\varnothing$
关系基本概念
定义: 给定任意集合A和B，若R$\subseteq$A$\times$B，则称非空集合R为从A到B的二元关系。
关系是一个集合，是序偶的集合。
二元关系： A=B时，称R为A上的二元关系
表示：
- 若(a,b)$\in$R，称a与b有关系R$\Rightarrow$aRb
- 若(a,b)$\notin$R，称a与b没有关系R$\Rightarrow$aR’b
三个特殊关系：
- 若R=$\varnothing$，则称R为A到B上空关系
- 若R=A$\times$B，称R为A到B上全关系 $U_A$
- 称R={(x,x)|x$\in$A}为A上的恒等关系 $I_A$
定义域： S中有序偶的第一元素组成的集合
值域： S中有序偶的第二元素组成的集合
关系的表示方法
集合法
列举法
例：“对号关系”
R={ (王一, 1), (李二, 2), (丁三, 3) }
描述法
例“对号关系” R的描述法表示：
A={ 王一,李二,丁三 }， B={ 1, 2, 3, 4 }
R={ (a, m) | a$\in$A, m$\in$B, m是a的学号 }
矩阵表示法
关系R可以用关系矩阵$MR=(r{ij}) {m*n}$表示:
$r{ij}=\left{\begin{array}{l}1, a_iRb_j\0, a_iR’b_j\end{array}\right.$
图表示法
关系R的图表示：用小圆点表示集合A、B中的元素；若aRb，则画一条从a指向b的有向边(弧)
例题
设A={-2,-1,0,1},写出A上的<关系，≤关系，全关系和恒等关系的关系矩阵、关系图
<={(-2,-1),(-2,0),(-2,1),(-1,0),(-1,1),(0,1)}
$M<=\begin{bmatrix}0&1&1&1\0&0&1&1\0&0&0&1\0&0&0&0\end{bmatrix}\$
$M\leqslant=\begin{bmatrix}1&1&1&1\0&1&1&1\0&0&1&1\0&0&0&1\end{bmatrix}\$
恒等关系：$M{I_A}=\begin{bmatrix}1&0&0&0\0&1&0&0\0&0&1&0\0&0&0&0\end{bmatrix}\$
全关系：$U_A$=A$\times$A $M{U_A}=\begin{bmatrix}1&1&1&1\1&1&1&1\1&1&1&1\1&1&1&1\end{bmatrix}$
关系的运算
关系的并、交、差、补
关系是序偶(有序对)的集合，因此可以对关系进行运算。若R, S$\subseteq$A$\times$B，则
R∪S， R∩S，~R，R-S$\subseteq$A$\times$B
复合运算
设R是一个从X到Y的关系，S是一个从Y到Z的关系，则R和S的复合关系：
R$\circ$S={(x,z)|x$\in$X,z$\in$Z,至少存在一个y$\in$Y,有(x,y)$\in$R且(y,z)$\in$S}
运算方法
画图
矩阵法：将进行复合运算的两关系用矩阵表示并$\times$乘，所得矩阵即为复合运算结果
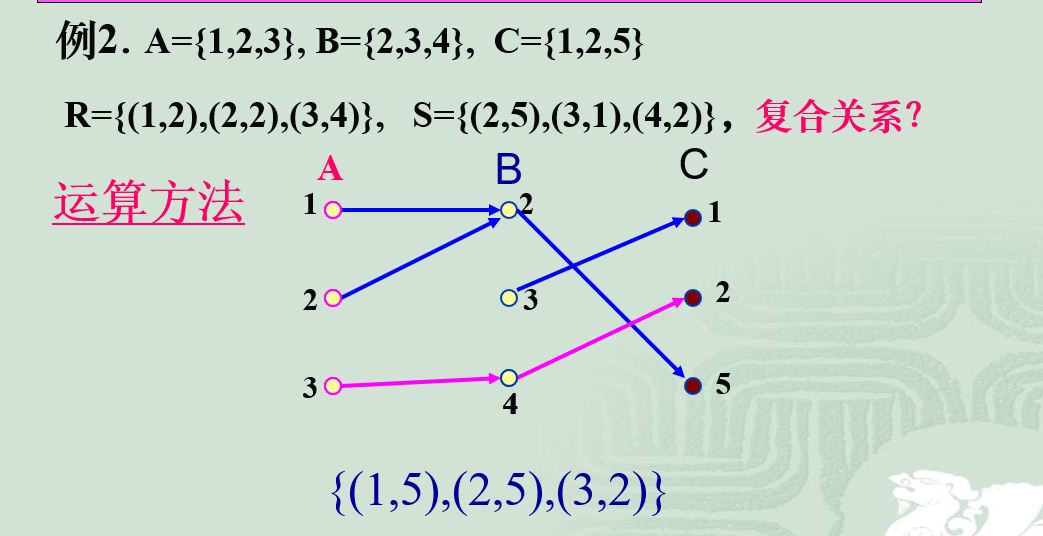
例3. A={1,2,3}, B={2,3,4}, C={1,2,5} ，R={(1,2),(2,2),(3,4)}, S={(2,5),(3,1),(4,2)}，复合关系？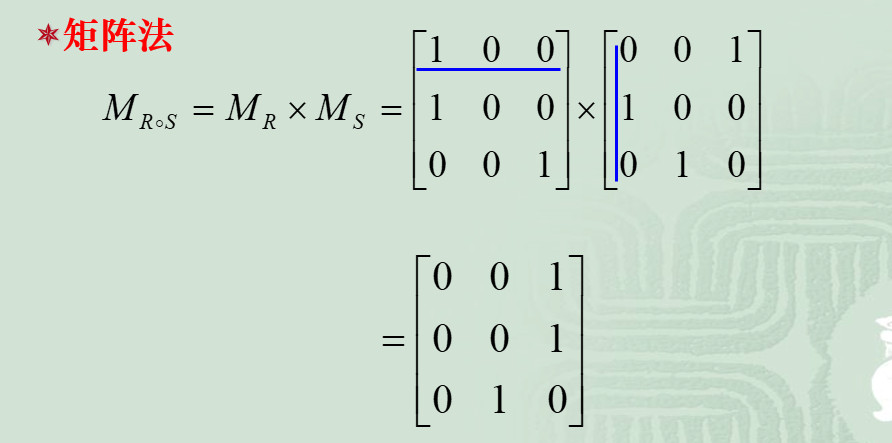

复合关系

定理2.1 设R、S、T分别表示从X到Y、Y到Z、Z到U的关系，则有
(R$\circ$S)$\circ$T=R$\circ$(S$\circ$T)
性质

$R^0=I_A$
$R^n+1=R^n $\circ$ R$
$R^n $\circ$ R^m=R^{n+m}$
$({R^m})^n=R^{m*n}$

逆关系

关系R的逆关系记为
$R^{-1}$={(b,a)|(a,b)$\in$R}
性质

$(R^{-1})^{-1}=R$
$(R\circ Q)^{-1}=R^{-1}\circ Q^{-1}$

关系的重要性质

自反与反自反

自反： 集合A的关系R，如对任意的x∈A，有(x,x)∈R，则称R是自反的。
$\Rightarrow$$𝐼_𝐴⊆𝑅$ （不能有序偶中的某元素在整个关系的序偶中成单出现）
反自反： 反自反：在集合A的关系R，如对任意的
x∈A，有(𝑥,𝑥)∉𝑅，则称R是反自反的
$\Rightarrow$$𝑅∩𝐼_𝐴=Φ$ (一个相同的序偶都不能有)

对称与反对称

对称： 在集合X上的关系R，如果有(x,y)∈R，必有(y,x)∈R $\Rightarrow$ $R=R^{-1}$ （有(a,b)就得有(b,a)成对出现）
- 若关系是对称的,其关系图中弧是成对的
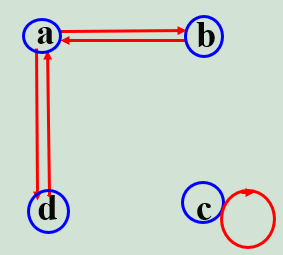
- 若关系是对称的，则关系矩阵是对称矩阵
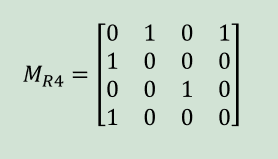
反对称: 在集合X上的关系R，如果有(x,y)∈R且x≠y，必有(𝑦,𝑥)∉𝑅
$\Rightarrow$$𝑅∩𝑅^{−1}⊆𝐼_𝑋$ （存在(a,b)而找不到(b,a)）
- 若关系是反对称的，关系图中无成对的弧
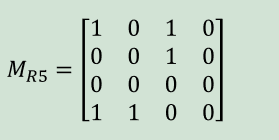
- 若关系是反对称的，关于主对角线对称的元素不同为1

传递

在集合X上的关系R，如果有(x,y)∈R且(y,z)∈R，则必有(x,z)∈R
$\Rightarrow$$𝑅^2⊆𝑅$

实数集合上的不同关系的性质

实数集上的”=”关系:自反、对称、反对称、传递
实数集上的”≤”关系:自反，反对称，传递
实数集上的”<”关系：反自反，反对称，传递
空集：自反，反自反，对称，反对称，传递

关系上的闭包运算

关系的闭包；使得关系满足特定性质的序偶集合

自反闭包：$𝑟(𝑅)=𝑅∪𝐼_𝑋$
对称闭包：$𝑠(𝑅)=𝑅∪𝑅^{−1}$
传递闭包：$𝑡(𝑅)=⋃{𝑖=1}^∞𝑅^𝑖$$=𝑅∪𝑅^2∪𝑅^3∪⋯$
若关系R为有限集合:$𝒕(𝑹)=⋃{𝒊=𝟏}^𝒏𝑹^𝒊$
传递闭包运算方法：求得$A$，$A^2,A^3$…当没有新的序偶出现时取并集
- $A^2=A\times A$, $A^3=A^2\times A$
- 利用画图，求$A^n$时，从某起点（作序偶第一个元素）出发经过可走路线n次到达的终点（作序偶的第二个元素）
  等价关系
  一个在X上的关系R，如果它是自反的、对称的、传递的，则为等价关系(x,y) ∈ R $\Rightarrow$ x~y
等价关系的关系图的特点：
(1) 分成一些块:等价类
(2) 每个块内的所有元素间均有关系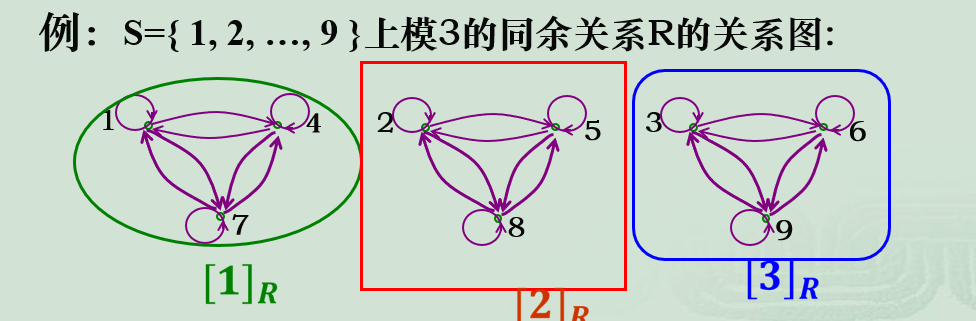

等价类

R是A上的等价关系, $\forall$a$\in$A, 可构造一个A的非空子集[a]R,称为由a生成的等价类

商集

设R为非空集合A上的等价关系，以R的所有等价类作为元素的集合，称为A关于R的商集，记以A/R。

划分

设S是一个集合，$A_1,A_2,A_3…A_n$ 是它的非空子集，如果满足条件：

(完整性) $U_{i=1}^m=S$
所有$A_i$ 间均是分离的，
即当$i\not= j$时，$A_i\cap A_j=\varnothing$则集合$A={A_1,A_2,⋯,A_m}$称称为S的一个划分。

偏序关系

集合X上的关系R是自反、反对称、传递的

偏序关系中的“可比”，“盖住”

若a,b之间有a≤b或 b≤a,则称a、b是可比的。
若a≤b且a≠b,且不存在另一元素c满足a≤c和c≤b，则称b盖住a。

哈斯图

1)用小圆圈作为结点表示集合中的元素
2)自反性不在图中表示出来
3) b盖住a，则a、b用线段连接 $\Rightarrow$b在上方，a在下方

偏序关系中的特殊元素

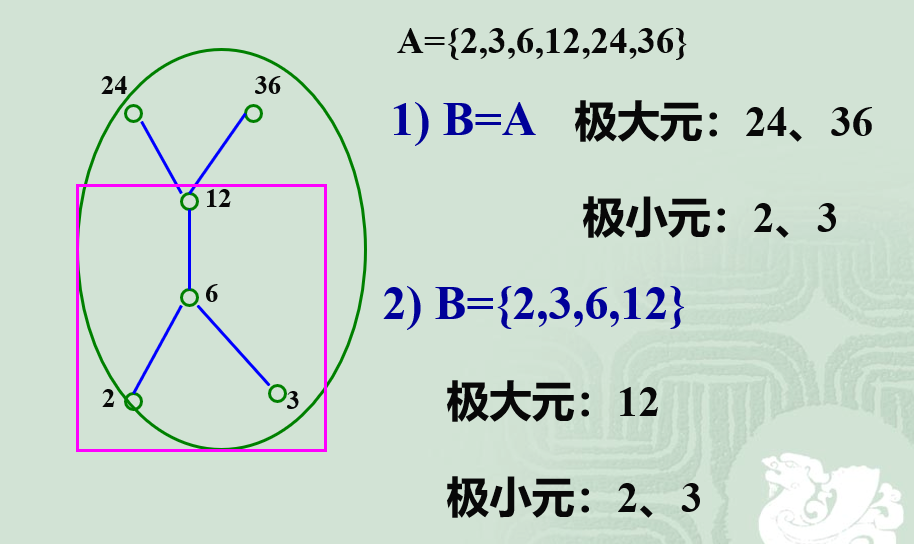
极大，极小元

极大元： 设集合A上的偏序关系“≤”，对集合 𝐵⊆𝐴若有a∈B，且不存在其他的元素x∈B，使a≤x。
极小元： 如果不存在元素y∈B，使y≤a，则称元素a为集合B的极小元。

最大，最小元

最小元素： 若有a∈B，使得对一切x∈B，有a≤x
最大元素： 若对一切x∈B，都有x≤a
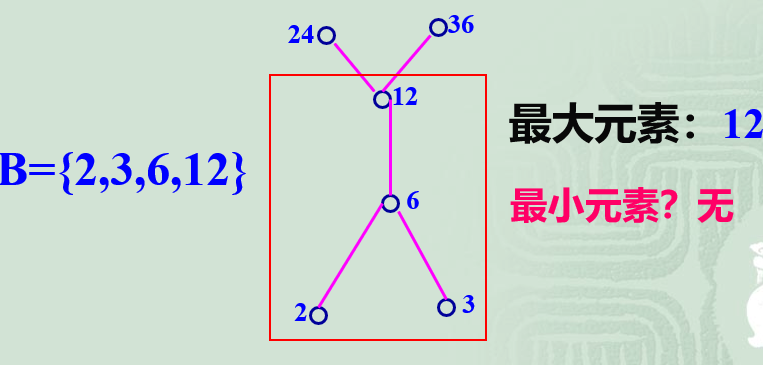
定理： 最大(小)元最多一个。

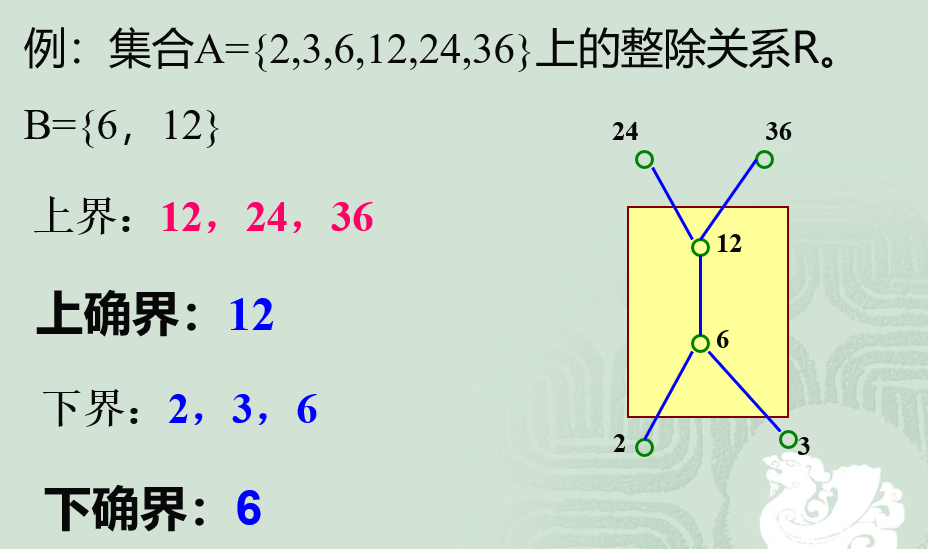
上下（确）界

下界：若有a∈A，使得对一切x∈B，有a≤x
上界：若a∈A，对一切x∈B，都有x≤a
下确界：下界中的最大元素
上确界：上界中的最小元素

【离散数学】关系

预备知识

笛卡尔乘积

关系基本概念

关系的表示方法

集合法

列举法

描述法

矩阵表示法

图表示法

例题

关系的运算

关系的并、交、差、补

复合运算